
3 June '04 Update
Reader Comments Page
In the area near Milan, the current (brown) plot roughly splits the 3.44 km difference between the green 24 May plot, and the yellow 1 June plot. The TLE used for this plot was posted earlier today by the MCC (the transit of Venus begins at about day-of-year 160.22):
1 25544U 98067A 04159.51932743 .00020000 00000-0 20000-3 0 9046 2 25544 51.6325 15.0272 0005564 207.3287 152.7581 15.68778822501504
An elevation of sea-level is assumed. I hope shortly to finish implementing the GTOPO30^ Digital Elevation Model, which will allow me to generate the transit track using accurate (to 30" resolution in latitude & longitude, or about 1 km at the equator) elevation data.
Microsoft Streets & Trips
... IssVenusTransit.est
file
(note the warnings about the 2004 S&T; I use S&T 2001 - email me for
where you can get S&T 2001 for $10 U.S. ;-)
The latest text file of Venus transit tick marks
(you may need to click Refresh to see the latest update)
1 June
The yellow plot, which has moved to within about a kilometer (in the area near Milan) of the blue plot from 20 May, is based upon the following TLE, posted today by the MCC:
1 25544U 98067A 04159.51921885 .00020000 00000-0 20000-3 0 9074 2 25544 51.6331 15.0248 0005532 209.7910 150.2937 15.68809969 36809
The green plot, which essentially splits the difference between the blue plot of 20 May, and purple plot of 17 May (anticipating an ISS orbit boost that occurred the following day), is based upon the TLE below, which was posted by the MCC on 24 May.
1 25544U 98067A 04156.58912257 .00020000 00000-0 20000-3 0 9127 2 25544 51.6329 29.9562 0005651 195.5451 164.5537 15.68675296 36340
20 May
Plotted below in purple is the ISS / Venus transit path computed on May 17. This plot presumably took into account the effect of the orbit boost scheduled for the following day. The blue plot is based upon a TLE posted by the MCC on May 20 (after the boost):
1 25544U 98067A 04152.51180967 .00020000 00000-0 20000-3 0 9110 2 25544 51.6346 50.7283 0005747 176.9937 183.1259 15.68565350 35705
The black plot is based upon the historic position of the ISS on April 28, when, according to the following analysis, its orbit should have corresponded closely (in average altitude & orbital period) to the orbit on June 8. The times given for this plot correspond to the ISS's position on April 28 (suitably "translated" to June 8, according to this analysis).
I believe that the principal value of this analysis & plot is to give some estimate of the expected error in the blue plot. In the area of northern Italy, for example, the black plot has moved about 6 km SE of the blue plot. Since the blue plot passes about 50 km NW of Monaco, for example, there's little chance that the actual (June 8) ISS / Venus transit track will end up in the Mediterranean, in this area. (Looking at the way earlier plots shifted around, a change of no more than 6 km seems quite optimistic, but the main point is that the final transit path should cross much of southern Europe.)
ISS TLE for 21 April, 1:32:26.064 UTC 1 25544U 98067A 04112.06419056 .00020000 00000-0 20000-3 0 9020 2 25544 51.6271 256.9057 0010993 52.4447 307.7710 15.68555744 29350 1:32:25 latitude -0.029095 longitude 24.307241 1:32:26 latitude 0.022567 longitude 24.343682 Now using TLE above 1:32:27 latitude 0.061244 longitude 24.372632 Interpolating, the equator crossing occurs at: 1:32:25.563 = TLE epoch - 0.501 seconds latitude 0.000000 longitude 24.327763 ISS TLE for 31 May, 12:17:00.355 UTC 1 25544U 98067A 04152.51180967 .00020000 00000-0 20000-3 0 9110 2 25544 51.6346 50.7283 0005747 176.9937 183.1259 15.68565350 35705 12:17:00 latitude -0.006037 longitude -22.863762 Now using TLE above 12:17:01 latitude 0.046125 longitude -22.825417 Interpolating, the equator crossing occurs at: 12:17:00.116 = TLE epoch - 0.239 seconds latitude 0.0000000 longitude -22.859324 So, the earth-referenced position at 0 seconds in the 31 May epoch corresponds to the position at -0.501 + 0.239 = -0.262 seconds in the 21 April epoch, but shifted west by 47.187087° The transit of Venus begins June 8, at 5:32:55 UTC, or DOY 160.231192, which is 7.719382 days into the 31 May epoch. The position of the ISS at that time should be close to the position 7.719382 days - 0.262 seconds = 7.719379 days into the 21 April epoch, which corresponds to DOY 119.78356999 (28 April 18:48:20.447). My archived MCC TLE preceding that date is: 1 25544U 98067A 04119.51743710 .00020000 00000-0 20000-3 0 9024 2 25544 51.6283 218.9203 0011040 78.8338 281.4063 15.68949863 30528 So, the position of the ISS at the start of the Venus transit should closely correspond to its position (shifted west) on 28 April, at 18:48:20.447 UTC. It should then be possible to estimate the ISS / Venus transit path for June 8 by computing the position of the ISS on April 28, shifting it west by about 47°, and computing the position of Venus 160.231192 - 119.783570 = 40.447622 days into the "future."

Here's a magnified view of the Mediterranean region:

Below is a further magnified view indicating the shift from the May 17 prediction to the May 20 prediction, along with the black plot that's based upon the position in orbit of the ISS on April 28:

Earlier discussion:
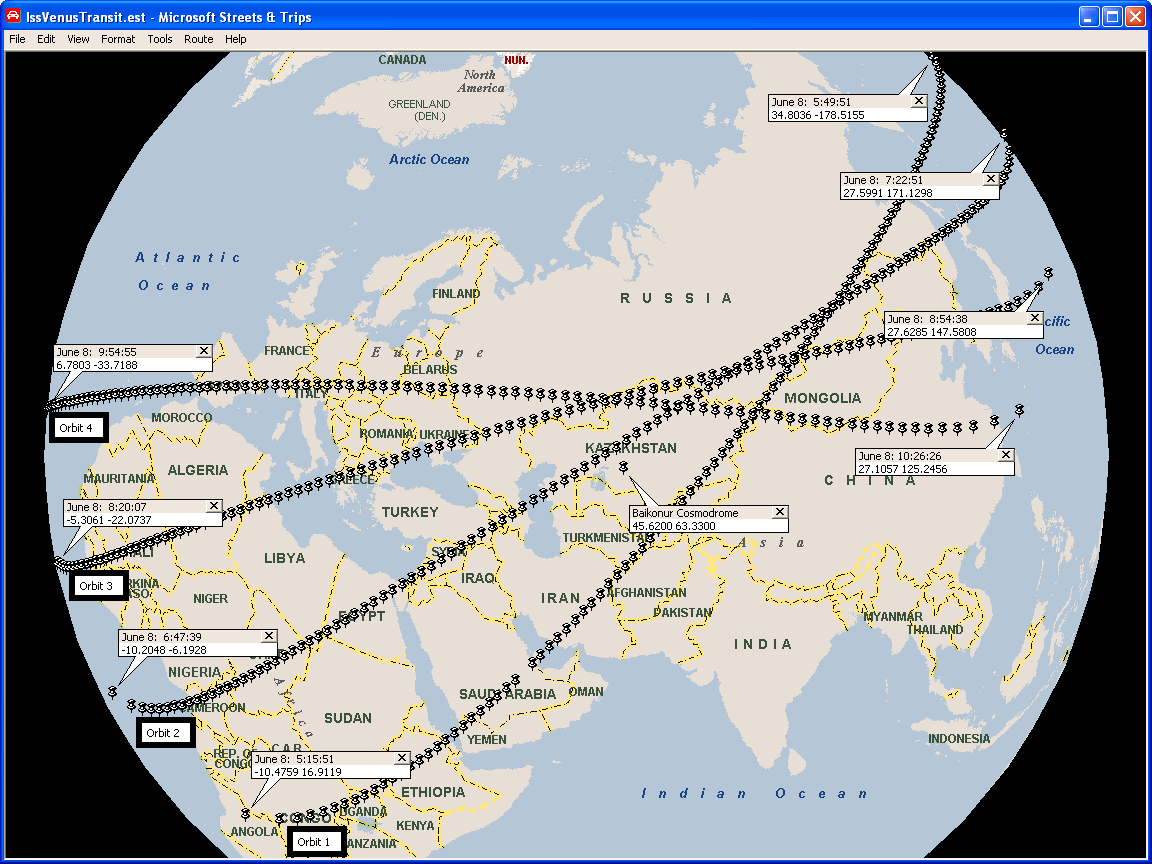
Below are 7 plots (times are UTC) of the predicted Venus-transit path of the ISS, during Venus' transit of the Sun on June 8. They were made using the latest NASA MCC ISS ephemeris; the black plot was made 5 Apr '04; the blue plot was made April 12; the green plot was made April 19; the yellow plot was made April 26; the red plot was made May 3; the brown plot was made May 10; and the purple plot was made May 17 (3 weeks and 1 day before the event, corresponding to about 352 orbits).
The Big Story here is the planned boost of the ISS's orbit tomorrow, lifting it into an overall higher & slower orbit, and ultimately causing a significant shift of the transit path to the northwest, relative to previously predicted transit paths in the area of Italy.
Another orbit boost between now and June 8 is highly unlikely, so my guess is that the actual transit path will end up near the currently predicted path ("near" is a relative term, of course- 160 km / 100 mi this way or that wouldn't surprise me). By next week, I think the final path should begin to come into good focus.
The regions of the transit path marked in red indicate that the elevation angle of the ISS (and the sun) at the time of the transit is at least 45°, which corresponds to a distance of about 312 miles / 502 km. The minimum distance to the ISS along the transit tracks is 254 miles / 409 km.
The orbit of the ISS has been declining for more than a year:

The decrease in altitude corresponds to a decrease in orbital period, which in turn means that the earth will rotate less (from west to east) from orbit to orbit (stated another way, the ground track of consecutive orbits will be nearer each other, where they cross the equator, for example), and consequently that the orbital path above the ground would seem to shift eastward (relative to an unchanging orbit).
Working against this effect, however, is the fact that the lower the orbit, the greater will be the rate of westward precession of the orbital plane, due to the earth's equatorial bulge. Evidently, with an orbit inclined to the equator at an angle of about 51°, these two effects must nearly cancel each other out, so that the track position remains about the same.
Because of this, it seems that one can now use these plots with some confidence (aside from the usual vagaries of weather) to plan an observing location, book a hotel room, etc.
The above sounds good, at least. In the zoomed view showing Italy, the blue plot at 9:27:10 is 52.2 miles west of the black plot at 9:22:48 (and 262 seconds delayed); the green plot at 9:31:12 is 103 miles west of the black plot (504 seconds delayed).
At a latitude of 41.4415°, (ignoring its oblateness) the earth is rotating at about 0.2174 miles per second (782.5 mph), so the shifted plots correspond to about 240 and 474 seconds worth of rotation; essentially the amount of delay between the plots. Furthermore, the fact that later plots (until the yellow April 26 plot) are delayed means that they actually represent higher orbits, rather than a declining orbit.
My guess, then, is that this "plot jitter" represents a small inaccuracy in the parameters in the TLE, such as that representing the orbital period.
These MCC TLEs evidently are produced from a prediction based upon numerical integration of accurate atmospheric & earth-gravitational models, which are then "dumbed-down" to SGP4 model TLEs. The MCC typically posts updates on Mondays and Thursdays, giving daily TLEs 11 days into the future.
I intend to do some tests to determine the long-range prediction accuracy of these TLEs. For example, the April 26 (day-of-year 117) plot is based upon the following TLE:
1 25544U 98067A 04128.56091372 .00020000 00000-0 20000-3 0 9119 2 25544 51.6255 172.7989 0011271 108.1472 252.0917 15.69336026 31948
which represents day-of-year 128, or May 7. I can use this TLE to compute a solar transit track for May 7, then on May 7 (using an up-to-date TLE), compute the actual transit track... and so on... so as to provide an estimate of what the long-range accuracy actually is.
The May 10 plot is based upon this TLE:
1 25544U 98067A 04142.56996404 .00020000 00000-0 20000-3 0 9115
2 25544 51.6262 101.3364 0010357 159.9249 200.2321 15.69517331 34140
May 17:
1 25544U 98067A 04149.70875706 .00020000 00000-0 20000-3 0 9120
2 25544 51.6304 65.0080 0005811 166.6668 193.4647 15.68392604 35268
On May 10, the TLE indicated 15.695 orbits per day;
the TLE used for the May 17 plot slows this down to about 15.684 obits per day.
The jitters... the following is a magnified view of these predictions in the area of Italy. The orbit boost that the ISS received on May 18 caused a large shift to the northwest, which is not shown here.

Busy, busy... the Weather Gods permitting... probably in the area of north central Kazakhstan (there is one ISS Transit subscriber in eastern Kazakhstan, about 1000 miles from Astana), one could observe simultaneous solar transits of Venus and the ISS, on consecutive ISS orbits. At 8:02:56 UTC, the ISS would also be quite high in the sky- at almost 58° elevation- and a distance of 268 mi / 431 km.

Meanwhile, that same day in Tuva...

Finally, transits on consecutive orbits may be observed in Russia, about 735 km ESE of Moscow, the second one occuring near the end of Venus' transit:

Michael Gill raised a question about the possibility of observing a transit of the ISS during the transit of Venus, June 8, 2004.
Here's a map of the region of the world where the transit of Venus will be visible (note the "sweet spot" near Oman):
And here's a bigger map.
2004 Transit of Venus gives the following times for the transit:
begin 5:32:55
UTC
greatest 8:19:44
end 11:06:33
Björn Gimle pointed out a critical error in my original analysis. My assumption was that:
The orientation of the ISS's orbit relative to the stars presumably will be very close to what it is today- as well as what it was on June 8, 2003 (i.e., it will have essentially the same inclination to the equator, the same orbital period of about 92 minutes, etc.).
In fact, due to the earth's equatorial bulge, each time the ISS crosses the equator (for example, going from north to south), it is deflected downward (i.e., toward the south, but also slightly downward in altitude) due to this concentration of mass. As it's pulling away from the equator, it's deflected upward (to the north- but it will also regain altitude as a result of the extra speed it picked up while losing altitude). The situation is similar to a light ray being shifted slightly in position, after passing at an angle through a glass plate, with the ultimate result that the orbital plane of the ISS precesses westward at a nearly constant rate of about 5.04° per day (or a full revolution in about 71.4747 days).

Above: the shifting of a ray of light as it passes at an angle through a plate of glass. The plane of orbit of the ISS precesses as if the ISS were a ray of light circling the earth, having to pass through a plate of glass each time it crosses the equator.
Rob Matson gives a mathematical description:
Nodal regression is a function of altitude and orbital inclination. The lower the altitude and the lower the inclination, the greater the nodal regression rate per day (the maximum possible is about 9°/day). The rate of change of the right ascension of ascending node (RAAN) due to earth's J2 zonal coefficient is given by:
delta Omega = -1.5 * n * J2 * (Re/a)^2 * cos(i) * (1-e^2)^-2
where n is mean motion in deg/day
Re is earth's equatorial radius
a is the semi-major axis in km
e is eccentricity
i is orbital inclination
J2 = .00108263
delta Omega is in deg/day
Since n is a function only of a, the formula can be simplified. After substituting all the constants, you get:
delta Omega = -2.06474E+14 * a^(-3.5) * cos(i) * (1-e^2)^-2
For a circular orbit, the last term is unity. So, try plugging in 51.6° for the inclination, and an altitude of 380 km (a=6758 km):
delta Omega = -2.06574E+14 * 3.94127E-14 * cos(51.6) = -5.06 deg/day
(the negative sign indicating westward movement of the RAAN).
The greatest problem confronting our attempt to forecast the ground track of the ISS (and its shadow / solar transit, on the earth's surface) months in advance is the uncertainty of the orbit itself. Below is a history of the ISS's orbital altitude, since its launch Nov. 20, 1998:
The Columbia tragedy (which did not follow a mission to the ISS) occurred at about week 220, and it's unlikely that a shuttle will visit the ISS prior to the Venus transit. As of this writing (Dec. 6, 2003), the ISS has fallen to its lowest mean altitude in about 2.75 years.
A declining altitude has as one consequence a shortened orbital period (the ISS will not only have less of a distance to travel, but will be traveling at a greater speed). Kepler's law that objects in orbit around a (much larger) object have a constant value for R3 / T2 can be used to determine the orbital period.
We can compute this value for the earth, since we know the earth's radius, and that the gravitational acceleration at its surface is 32.2 ft / sec2 (9.8 m / sec2).
Imagine the Starship Enterprise flying in a circular orbit at the earth's surface ("atmospheric & mountain deflector shields ON!"). We define our coordinate system so that at t = 0, the Enterprise (orbiting in our XY plane) is moving at velocity V at X = 0, Y = 3956.538 miles. Half an orbit later ( T / 2 ) at X = 0, Y = -3956.538 miles, the Enterprise will still be going at a speed of V, but will in the opposite direction (hence, at velocity -V), having changed it's velocity (due to the earth's gravitational acceleration) by 2 * V. So in 1 full orbit (taking time T), it will change its velocity by 4 * V.
acceleration = 4 * V / T (period of orbit) = 32.2 ft / sec2
Now the velocity V is just = 2 * Pi * 3956.538 * 5280 / T (there are 5280 feet in a mile)
so 32.2 ft / sec2 = 4 * ( 2 * Pi * 3956.538 * 5280 / T) / T = 525,036,049 / T2 = ( 2 * Pi * 3956.538 * 5280 / T)2 / (3956.538 * 5280)
and T = 4038 seconds = 67.3 minutes
Well, that was a nice argument, but something's wrong with it. The correct equation for centripetal force (the force required to cause something moving to move in a circle) is:
acceleration
= V2 / R = (2 * Pi * 3956.538
* 5280 / T)2
/ (3956.538 *
5280)
=
and T = 5061 seconds = 84.3 minutes
This is the same value as computed below.
We can compute this value for the earth given that the orbital altitude for a geosynchronous satellite is 22,237 miles (35,787 kilometers), giving an R (after adding in the average radius of the earth, from the chart below) of 26,194 miles (42,154 km).
| Size and shape of the Earth | ||||
| polar | equatorial | difference | average | |
| Earth's radius (mi / km) | 3949.894 / 6356.751 | 3963.181 / 6378.135 | 13.288 / 21.384 | 3956.538 / 6367.443 |
|
" diameter |
7899.787 / 12713.501 | 7926.363 / 12756.270 | 26.575 / 42.769 | 7913.075 / 12734.886 |
Roughly speaking, the earth is about 25 miles / 40 kilometers fatter at the equator than at the poles. One could think of this as being a 13 mile- high mountain range encircling the equator (cf., the summit of Mt. Everest is 29,035 feet above sea level = 5.50 miles).
The T for a geosynchronous satellite isn't 24 hours, however, because in one day, the earth (and any geosynchronous satellite) rotates not 360°, but 360° + the amount of an orbit about the sun that the earth completes in a day. Since the earth travels 360° around the sun in about 365 days, this amounts to about 1 degree per day (and explains why stars rise about 4 minutes earlier, each evening: 1 / 360 of a circle * 1440 minutes per day = 4 minutes). A more precise value for T is given by:
T = 1440 minutes / ( 1 + 1 / 365.2422) orbit = 1436.07 minutes orbital period giving: R3 / T2 = 8,714,758 mile3 / min2 or T = Sqrt(R3 / 8,714,758) min
Using this figure, the chart below gives the orbital period for various altitudes:
| altitude (miles) | orbital period |
| 0 (orbit at earth's surface) | 84.3 min. |
| 100 | 87.5 |
| 230 (370 km) | 91.8 |
| 242 (390 km) | 92.2 |
| 26,194 (geosynchronous orbit) | 1436.1 |
| 238,896 (avg. distance to the moon) | 27.5 days |
In regard to the moon, I'm assuming that the "average distance" is measured from center to center, rather than surface to surface. This 27.5 days (a more accepted figure appears to be 27.3 days) is the "sidereal period;" that is, the orbital period relative to the stars. To get the synodic period- which is the time from full moon to full moon (i.e., a month)- one has to add in an extra amount to compensate for the earth's approximately 28° of travel around the sun during that time.
Basically, if there were precisely 12 months in a year, the moon would have to make precisely 13 orbits of the earth (relative to the stars). Given a "sidereal month" of 27.5 days, we calculate that the moon makes 365.2422 / 27.5 = 13.30 orbits of the earth per year. So,
1 month = 27.5 days * (13.30 sidereal months / 12.30 synodic months) = 29.7 days
(The accepted figure appears to be 29.5 days... the figure I use for the altitude of geosynchronous orbit may not be correct; the figure I remember- and have seen references to in my Google search- is 22,400 miles, rather than 22,237. However, I think the "problem" may be that the moon isn't all that small; the earth and moon actually orbit about each other, at a point which I calculate to be near the earth's surface- which of course causes high ocean tides on the side of the earth that's away from the moon.)
I'm attempting to try to forecast the orbit of the ISS 175 days in advance. During that time, it would make 2745.1 orbits if it maintained an altitude of 370 km, and 2733.2 orbits at 390 km; or about 12 orbits more, at the lower altitude. This means that- even if we can reasonably estimate the orbital plane- we can have no idea exactly where the ISS will be in its orbit at 8:19:44 UTC on June 8, 2004.
However, the changing altitude also affects the rate of precession. At 71.4747 days per "revolution," the ISS will precess 2.45 revolutions in 175 days. Even a modest error in the precession rate, of 1 part in 245, will result in a difference of .01 revolutions, or 3.6°- further adding to the problem of not being able to make a long range estimate of where the ISS will be in its orbit.
If the orbit were being maintained near an average altitude of 390 km- as it was for nearly 2 years- then we'd have a better chance of figuring out in advance where to observe an ISS transit the sun during the transit of Venus.
This is a bit of a digression, to show that the position of the sun in the sky at 8:19:44 UTC on June 8, 2004, will be essentially the same as it was at 8:19:44 UTC on June 9, 2003...
A fairly well known astronomical phenomenon is the analemma- represented by the photograph below- which is a composite photograph made by photographing a particular region of the sky (apparently near sunrise or sunset) taken at a particular time of day, throughout the course of a year:
It's shape (which was originally explained to me by Eugene Shoemaker- who seemed to appear behind me from nowhere- as I was looking at a sundial that used to be on the Caltech campus) depends upon the inclination of the earth's axis to its plane of orbit (thus, the up & down movement of the sun during the year); the fact that the earth's orbit is slightly elliptical (having a perihelion of about 91.5 million miles on about January 2, and an aphelion of about 94.5 miles on about July 4) which means that- because of Kepler's law that an object in orbit sweeps out equal areas in equal amounts of time- the sun appears to move faster in the sky on January 2 than on July 4 (which largely accounts for the figure 8 being skinny at the top, and fat at the bottom).
The final dependency is the relationship of the Vernal Equinox to the perihelion. This has a somewhat subtle, "mathematical" effect, which actually isn't hard to understand: if you imagine flying an airplane around the earth, passing near the poles (but not right over them) along the way, then as you fly near the poles (without changing speed) you are changing your longitude quite quickly. On the other hand, as you cross the earth's equator (headed very nearly north from south), you're changing latitude quickly, but longitude hardly at all.
Because of the tilt of the earth's axis, the sun would move more quickly in Right Ascension (the celestial equivalent of longitude) near the solstices (where the sun "flies" closest to the celestial poles) than near the equinoxes (where the sun crosses the celestial equator), even if the earth's orbit were circular.
So, the analemma slowly changes shape over the course of the 26400 years that it takes for the earth's axis to precess a full revolution. This means that the analemma changes very little from century to century, let alone, from year to year. It can therefore be used as the basis for an accurate sundial- or more nearly sun-bowl, as the one at Caltech was constructed.
Now, a "solar year" is about 365.2422 "mean solar days," so 4 years is about 1460.97 days. This means that the position of the sun at 8:19:44 UTC on June 8, 2004, will be almost precisely what it was 1461 days earlier, at 8:19:44 UTC on June 8, 2000.
At 8:19:44 UTC on June 9, 2003- 365 days before 8:19:44 UTC on June 8, 2004 (a leap year)- the sun's position in the sky won't be quite as nearly the same, but still it will be quite close. June 8 is near the summer solstice (about June 22), and the sun's declination will be close to 23°. However, the sun will be about .25° (i.e., half a sun diameter) "less to the east" in 2004, due to the fact that the last .2422 day of the intervening year has yet to pass (and the sun moves about 1 degree in the sky each day).
Therefore, a computer program could make June 9, 2003 "look like" June 8, 2004 (in terms of how the earth would appear, as seen from the sun) just by "moving" the sun .25° to the west, from where it actually was on June 9.
Now, we'd actually need to use a TLE prior to 5:32:55 UTC, June 8, 2004, to compute the position of the ISS for that day; which means a TLE of about DOY 160.2 or before.
Likewise, we need a TLE prior to 5:32:55 UTC to compute the ISS's position prior to 5:32:55 UTC, June 9, 2003 (the date we intend to use to "fake" June 8, 2004). The TLE meeting this criterion, which I have archived, is:
1 25544U 98067A 03159.50375014 .00041100 00000-0
34010-3 0 9024
2 25544 51.6329 63.8779 0006615 228.9044 131.1541 15.59296411
19655
(which corresponds to about 12 hours UTC, June 8). The principal problem with using this TLE is that it doesn't correctly represent the ISS's plane of orbit for June 8, 2004, because of precession.
As of this writing, the most current TLE is:
1 25544U 98067A 03349.56891005 .00014961 00000-0 18257-3 0 9114
2 25544 51.6262 184.8183 0006263 256.3406 103.7055 15.65848435 9368
(which is 175 days before the Venus transit). If we turn the clock back to 349.50375014 (using the fractional part of the June 8 TLE), the RAAN will become:
184.8183 + 360 * (.56891005 - .50375014) / 71.4747 = 185.1465
allowing us to transform the above (in regard to RAAN) to:
1 25544U 98067A 03349.50375014 .00014961 00000-0 18257-3 0 9114
2 25544 51.6262 185.1465 0006263 256.3406 103.7055 15.65848435 9368
Now, 349 - 159 = 190 days, so to make a best guess at the RAAN for June 8, 2003 + 365 days, we need to precess the above by 365 - 190 = 175 days:
360 * 175 / 71.4747 = 881.4308 = 720 + 161.4308
which gives 185.1465 - 161.4308 = 23.7157
our "fake" TLE then becomes:
1 25544U 98067A 03159.50375014 .00041100 00000-0
34010-3 0 9024
2 25544 51.6329 63.8779 -> 23.7157 0006615 228.9044 131.1541 15.59296411
19655
Björn's suggestion for June 7, 2004 was:
ISS Venus
1 25544U 98067A 04159.33513226 -.00000042 00000-0 -33560-6
0 8400
2 25544 51.6298 18.6515 0006280 188.6155 171.4733 15.65067524316736
which we can transform to:
1 25544U 98067A 04159.50375014 -.00000042 00000-0 -33560-6
0 8400
2 25544 51.6298 17.8022 0006280 188.6155 171.4733 15.65067524316736
Björn's RAAN is thus 5.9135° "more precessed" than my best guess, corresponding to slightly more than 1 day.
This has things looking fairly good for the folks in Europe; at 8:16:49 UTC (near the time of greatest transit), with the ISS headed to the northeast (gold dot is ISS; white dot is solar transit point):

On the following orbit, at 9:52:09 UTC:

As Björn had suggested, "It may make nice NB passes over Oman, Egypt, Greece, Spain-Italy during the transit!" (I'm not sure what "NB" means - Kevin Fetter seems to have figured it out: "north bound")
Presently, it looks unlikely that, during the Venus transit, an ISS transit could be observed as far north and west as Spain, however.
Or, we could just try Björn's suggestion:
ISS Venus
1 25544U 98067A 04159.33513226 -.00000042 00000-0 -33560-6
0 8400
2 25544 51.6298 18.6515 0006280 188.6155 171.4733 15.65067524316736
Or, we could just "run with what we've got":
the latest NASA MCC TLE, propagated forward 6 months! Amazingly, that
gives precisely the same results as using Björn's
"ISS Venus"
(add 4 hours to the time field, to convert to UTC).
6:25:01 UTC; India may be a good place to be, for transit enthusiasts:
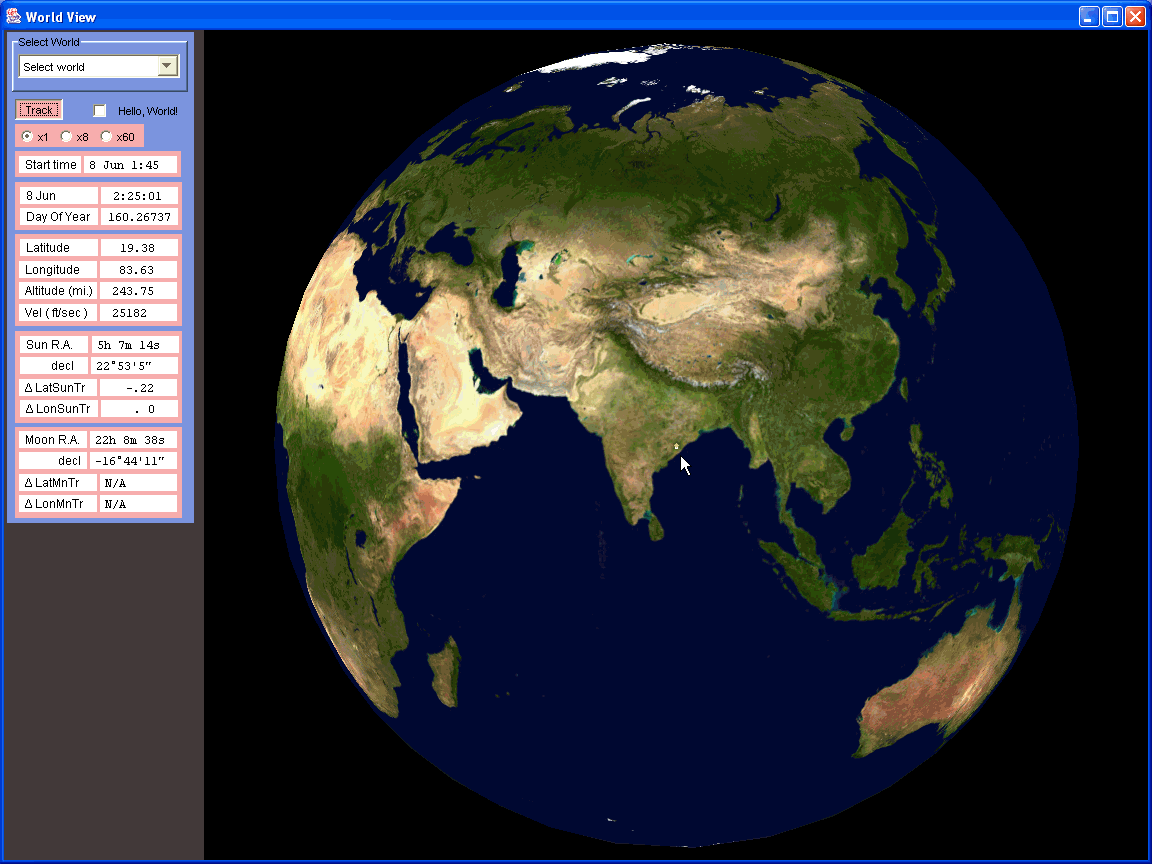
7:42:15 UTC (gold dot is ISS; white dot is solar transit point; red dot is lunar transit point); South Africa may be a better place to be (probably much cooler than India!):

7:57:26 UTC, the sun (and Venus) are almost directly overhead from the ISS:

So, which to believe (if any of the above)? If anybody wants to make a bet, I believe I'll bet on the Mediterranean area, somewhat east of Spain.
Older stuff:
The "greatest" part of Venus' transit will occur at 8:19:44 UTC. Now, it takes the earth 1 sidereal (?) year to complete 1 orbit of the sun (e.g., from perihelion to perihelion- which occurs on about January 2). A solar year is about 20 minutes less than this (roughly 525600 minutes per year divided by the 26400-year period of retrograde precession of the earth's axis), so it takes about 1 year and 20 minutes for the earth to complete an orbit of the sun (i.e., leaving the earth & sun in the same relationship, relative to the stars).
We need to keep in mind that a "solar year" is about 365.2422 "mean solar days" = 365 days, 5 hours, and about 49 minutes- so it takes 365 days, 6 hours, and about 9 minutes for the earth to complete 1 orbit of the sun.
We also need to remember that- since 2004 is a leap year- there are 366 days from 8:19:44 UTC June 8, 2003, to 8:19:44 UTC June 8, 2004; this represents about 17 hours and 51 minutes longer than the time required for the earth to orbit the sun.
So at the time of the "greatest transit" of Venus in 2004, the earth & sun will be in the same orientation, relative to the stars, as they were at about 2:10:44 UTC, June 9, 2003 (except that the earth's axis will have wobbled slightly, and the earth itself will be 6 hours and 9 minutes "more rotated" in 2004); consequently, at the time of the "greatest transit" of Venus, the sun-earth-ISS relationship essentially will be the same as it was at 2:10:44 UTC, on June 9 of this year (or 22:10:44 Eastern Daylight Time, June 8).
To have a look at that relationship, I started WorldView with a date of 8 PM EDT, June 8, 2003, and let my Pentium 3 spin its electrons & holes* for a while.
At 2:02:17 UTC, June 9, 2003, the ISS was about 500 miles northeast of Guam, with the sun almost directly overhead (less than 4° north of the zenith), and was generally heading north and east:

10 minutes later, it was about 500 miles south of the Aleutian Islands (the gold dot is the ISS; the white dot is its "shadow" on the earth's surface- where you'd observe it transiting the solar disk):

At 2:10:44 UTC + about 6 hours (i.e., at 8:12:00 UTC on June 9, 2003) the sun-earth-ISS relationship essentially was the same as it will at 8:19:44 UTC on June 8, 2004, and the earth's rotation will be essentially the same (less rotated, in 2003, by about 8 minutes). The screen capture below shows that, this past June 9, the ISS was over Oman, again with the sun nearly directly overhead, and generally headed north and east.

That, however, probably isn't where the ISS will be at 8:12:00 UTC on June 8, 2004- it could be anywhere in its 92 minute orbit (the worst case is +/- 46 minutes). Nonetheless, it appears guaranteed that at 8:12:00 UTC +/- 46 minutes on June 8, 2004, the ISS will be at a latitude of about 21° north, with the sun very nearly overhead.
The bad news, for a lot of SeeSat-L folks, is that the ISS isn't headed their way, from Oman. However, on the previous orbit- prior to Venus' greatest transit- those in India may be in luck.
Anyone wishing to top Roland Stalder might try making a movie showing the ISS occulting Venus, during its transit of the Sun.

(Credit Playboy magazine 1979)
"Phfttt! Our Beatles beat your precious
Rolling Stones any day!"
- Homer Simpson (vacationing in England)
* including one in its shoe